Magazine Archive
Home -> Magazines -> Issues -> Articles in this issue -> View
Tuning Fork | |
Article from International Musician & Recording World, August 1975 | |
End arguments about concert pitch. Build our electronic tuning fork.
Every player of a stringed instrument which requires tuning regularly will be aware that both pitch pipes and tuning forks are a less than ideal reference source.
The pitch pipe is not very stable because the breath moisture condenses on the reeds, increasing their mass, thus making the pitch drop a small, but important, amount. A tuning fork requires but one hand to use, thus leaving only one hand to play the string and adjust the machine head: This is not very easy.
The obvious answer is a self sustaining tuning fork, or a fully electronic equivalent, which can feed through a guitar amplifier.
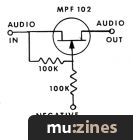
The unit described here is an oscillator, known as a 'Wein bridge'. This has been chosen because it can have a frequency stability of approximately 0.1%, which is equivalent to a pitch stability of about 1/60th of a semitone. Although not as precise as a laboratory tuning fork, it is far better than pitch pipes, and can be 'tuned' far more accurately than a tuning fork — which keeps fading out.
Readers who are familiar with normal Wein bridge oscillators will notice that the unit described here has the traditional thermistor replaced with two diodes and some resistors. This is done purely to reduce costs, resulting in a unit which should not cost more than £1 to make.
All the components required are of very easily obtainable types but special attention should be given to getting the best quality components for those parts which set the pitch. These are C1, C2, R1, R2 and VR1.
'Metal oxide' or 'Metal film' resistors are best but carbon film resistors will do. Solid carbon types should not be used for either of these resistors. The capacitors should be of polyester or polycarbonate film types. VR1 should be of the cermet type or of the small wirewound type. A carbon pot in this position is unlikely to be satisfactory.
VR1 sets the pitch of the oscillation and is chosen to have enough range to set the oscillator pitch to the 'E' of the open first string of a guitar with component tolerances given, providing all the components valves are not simultaneously at their limits. If you should find insufficient tuning range, a high valve resistor (100k) connected across R1, if the pitch is too low, or changing to R2 to 18K if the pitch is too high, should solve the problem.
VR2 sets the level of oscillation; if it is set at the top end, the unit will not oscillate at all and if set at the lower end, the oscillation is too fierce, distorted and out of tune.
The correct setting is a little past the point where the oscillation first starts but does not advance, so the sound becomes harsh.
Construction can be by any standard technique but the layout given is for plain (not copper) Veroboard or Lectrokit board and pins. On this layout, none of the wires on the back of the board cross, so it can be connected up with uninsulated tinned copper wire. For the enterprising constructor, the layout could be connected directly to a printed circuit, using any one of the printed circuit kits which are on the market.
No box details are given because I am sure each constructor will have his own ideas about fixing it into an existing piece of equipment or into the headphone amplifier unit described last month.
Battery consumption is about 4 MA from each battery and, because one would not expect to spend all evening 'tuning up', the battery life can be expected to be not much less than its normal shelf life.
Setting up is best done using a normal tuning fork, if an E tuning fork is available. Setting up by tuning for a 'nice round sound' with an A or C tuning fork is not perfect because one cannot take into account the errors of tempering the scale. For normal musical pitch A = 440 Hz and E = 329.63 Hz. Using this figure, the unit can be adjusted by employing a frequency counter if you have access to one.


THEORY
"It's good enough for Jazz"
The human brain likes, and actively seeks out, orderliness in all it surveys.
The main difference between musical noise and unmusical noise is the degree of orderliness apparent in the musical noise and the random nature of non-musical noises.
This can be most easily demonstrated by attaching a writing stylus to an ordinary tuning fork and exciting the fork whilst simultaneously moving a sheet of paper under the fork, as illustrated, at a FIXED speed.

The absolute symmetry of the pattern thus created on the paper sheet tells us a lot.
Firstly: Even though the tuning fork was excited by blows of very different velocities and directions, the number of patterns (or cycles) per inch of paper never varies.
Secondly: Even as the tuning fork settles back to zero movement, the number of patterns per inch of paper remain constant but at a reduced and regularly diminishing width or amplitude.
From this we can deduce that the note created with the tuning fork, (in this particular instance A=440) draws 440 complete sine-waveforms (pure tones) in every complete second of oscillation regardless of the strength of the blow used to excite it and continues to do so until almost the point where all its energy is dissipated and it comes back to rest.
Without going into long and laborious proofs, which have been done many times by various physicists, we are going to ask you to believe the following ideas.
A) Any object, when excited, will vibrate at a frequency (speed) relative to its SIZE, WEIGHT and Density . This we will call its RESONANT FREQUENCY.
B) If an object vibrates at a given frequency, it will give off, by vibrating the air around it, a sound at a given pitch.
C) The words FREQUENCY and PITCH have different meanings. Anything vibrating at a given frequency can be measured whereas a note of a given pitch is only 'sensed' by our hearing apparatus and can be inaccurate or fool our ears with the presence of confusing noises or even by a difference in the amplitude (amount) of sound being 'sensed' (heard).
D) So far we have talked only of pure tones. (Sinewaves to the engineer, flute or Tibia tones to the musician).

Sine Wave
How do I get my instrument in tune?
Like many problems, the answer is to understand the problem and you will have solved it.
The notes of the scale are not a random selection. One thing all the various 'Scales' used by different cultures around the world through the ages have in common is that the frequencies of the notes in the scale (we use a 12-note scale) are always related by simple whole number ratios. We know, from experience, that this gives the sounds people prefer.
If, for example, we play a 'C' and find it has a frequency of 261.6 cycles (waveforms) per second (now — confusingly — called Herz), we will find that the 'C' one octave higher has a frequency of exactly double the number, namely 523.2 Herz. A simple ratio of two to one (2:1).
If we count the frequency of the 'G' between these two 'C's, we will find it has a frequency of 391.9 a simple ratio of one and a half to one (3:2).
If we therefore divide the octave into twelve equal divisions, we will, in theory, end up with a perfect scale of semi-tones. In order to achieve this end, we divide the frequency from which we decided to start (a tuning fork of A=440 Herz is a common one), by the 12th root of the simple octave ratio 2.
This constant figure comes out at 1:1.0594631 (correct to seven decimal places). To save time, the figures come out thus:—
| A | 440 Herz. |
| A Sharp | 466.164 Herz. |
| B | 493.883 Herz. |
| C | 523.251 Herz. |
| C | 523.251 Herz. |
| C Sharp | 554.365 Herz. |
| D | 587.330 Herz. |
| D Sharp | 622.253 Herz. |
| E | 659.255 Herz. |
| F | 698.456 Herz. |
| F Sharp | 739.989 Herz. |
| G | 783.991 Herz. |
| G Sharp | 830.609 Herz. |
| A | 880. Herz. |
(Because we have limited the number of decimal places to seven digits, a small error of insignificant proportions can become apparent in these figures.)
From these figures we can see that the following simple ratios of frequencies occur:
| Octave Interval | 2:1 |
| Fifth Interval | 3:2 |
| Fourth Interval | 4:3 |
| Sixth Interval | 5:3 |
| Major Third Interval | 5:4 |
| Minor Third Interval | 6:5 |
| Major Second Interval | 11.10 |
If we calculate the figures, starting from another note, we will find that, using the same method of calculation, the frequency we get for each note will be slightly different from those calculated, starting from A=440. Because the mathematical (perfect) method of arriving at our scale gives us numbers that are not EXACTLY whole number ratios, for example 1½ x 440 = 660 whereas, we calculate the note E as being 659.225 Herz, an 'error' of very great significance to the musician has occurred.
This is why a piano tuner, if asked, would tell us that perfect tuning is possible in only one key at a time.
To arrive at a workable solution to the tuning problem, a compromise has been reached whereby the tuner will 'temper' his tuning to be somewhere in the middle of the twelve possible frequencies which each note would need to be tuned to if every key was to be in 'perfect' tune.
Components List
| Ref. | Value | Rating | Tol. | Notes |
|---|---|---|---|---|
| R1 | 15K | ¼ W | 5% | Metal oxide film are best for R1 & R2 |
| R2 | 15K | ¼ W | 5% | |
| R3 | 10K | ¼ W | 5% | |
| R4 | 4K7 | ¼ W | 5% | |
| R5 | 150K | ¼ W | 10% | |
| R6 | 15K | ¼ W | 10% | |
| R7 | 1K | ¼ W | 10% | |
| C1 | 0.033 uf | 10% | Polyester or polycarbonate film type | |
| C2 | 0.033 uf | 10% | ||
| D1 | IN 914 | Any general purpose silicone diodes | ||
| D2 | IN 914 | |||
| IC1 | uA741 | |||
| VR1 | 5K preset | Cermet | ||
| VR2 | 470K | Carbon or cermet |
More with this topic
The Syndrom - How it Works (Part 1) |
Bionic Trumpet |
Constructing A Trigger Delay |
Chip Parade (Part 1) |
The Ultimate Blinky Light - LED Wall Art - Visual Environment Machine |
Amdek Hand Clapper Kit |
Short Circuit |
The Miniblo |
Electro-Music Engineer - Tuning Up — A Review of VCO Calibration Methods (Part 1) |
Experimenters Circuits - Using The CA3080 |
To Phase or to Flange - Or To Each His Own |
Magic Buttons - Touch Switch Theory |
Browse by Topic:
Electronics / Build
Publisher: International Musician & Recording World - Cover Publications Ltd, Northern & Shell Ltd.
The current copyright owner/s of this content may differ from the originally published copyright notice.
More details on copyright ownership...
Feature
Help Support The Things You Love
mu:zines is the result of thousands of hours of effort, and will require many thousands more going forward to reach our goals of getting all this content online.
If you value this resource, you can support this project - it really helps!
Donations for April 2024
Issues donated this month: 0
New issues that have been donated or scanned for us this month.
Funds donated this month: £7.00
All donations and support are gratefully appreciated - thank you.
Magazines Needed - Can You Help?
Do you have any of these magazine issues?
If so, and you can donate, lend or scan them to help complete our archive, please get in touch via the Contribute page - thanks!